Hello everyone,
I share herein one of my laborius studies of this term. I havent actually made much of coding. It was given us by our distinguished, helpful professor 🙂 . It was my MAT 509 project and we tried to model heisenberg magnet under the effect of different parameters to see thickness dependent curie temperature shift on the magnet.
We made two dimensional grid and worked it out for two dimensional space. So, eventhough heisenberg is a method of n-vector models with three dimensional space we used two dimensional x-y model of magnetism. Energy calculation was made accordingly and monte-carlo simulation has been worked for it. As well known, it is simple algorithm and method to calculate or predict the state of near future for randomly distributed systems. There are many examples of monte carlo method in Landau physics or molecular dynamics.
We used the mean field theory, also known as self-consistent field theory to calculate energy values for atoms. Mean field theory was taking only nearest neighbouring interaction into account and neglecting the others.
So I write below our project report and heisenberg code with its explanation. Hope you find it helpful. Again, to remind, this code didnt come out from my brain. 🙂 But I do think that people may need somehow to start from somewhere for run similar problems since it is not easy to find related topics on the web-mass. Last to say, I have worked for this project with my distinguished colleagues, Aslıhan and Çağatay. Thanks again folks 🙂
___________________________________________________________________
Contents
Contents. 1
ABSTRACT. 2
OBJECTIVE. 2
1. THEORETICAL BACKGROUND.. 3
1.1. Magnetism.. 3
1.2. n-Vector Models. 3
1.2.1. Classical Heisenberg Model 3
1.3. Monte Carlo Simulation. 3
2. COMPUTATIONAL STUDY. 4
2.1. Generic of the Code. 4
2.2. Initial Conditions. 4
2.3. Curie Temperature. 6
3. CONCLUSIONS. 9
4. REFERENCES. 10
Within the context of this project, 2D Heisenberg magnet was modeled by using Monte-Carlo simulation. During this study; average Tcurie (transition temperature) was found by modeling the system with a defined boundary conditions. Modeling was performed by using MATLAB software. Curie temperature changes with respect to thickness of that given system had been shown through the medium of mean field approximation.
In our study, it is assumed that the structure is simple cubic, same approach can be used to model different crystallographic structures with an update on the energy formulation by changing the interatomic distances. Temperature transitions and magnetic susceptibility calculations were performed for 10 -20-30 cells and 5-12-19 cells respectively.
OBJECTIVE
Aim of the study covers the appreciated understanding of classical Heisenberg formulation and its application to model different behavior of ferromagnetic materials as a function of various extensive parameters such as external magnetic field, lattice thickness, interaction strength of spins and etc. By performing the analysis at fixed thickness, general behavior of system is understood and by plotting the spin components of lattice sites (for each atoms), natural tendency of the system is observed.
Modeling of thickness dependence of the ferromagnetic materials has been capturing attention recently, especially for thin film studies to have a deeper understanding of quantum mechanical phenomena which lays behind the magnetism.
1. THEORETICAL BACKGROUND
1.1. Magnetism
Magnetism is a property of materials that respond at an atomic or subatomic level to an applied magnetic field. Ferromagnetism is the strongest and most familiar type of magnetism. It is responsible for the behavior of permanent magnets, which produce their own persistent magnetic fields, as well as the materials that are attracted to them. However, all materials are influenced to a greater or lesser degree by the presence of a magnetic field. Some are attracted to a magnetic field (paramagnetism); others are repulsed by a magnetic field (diamagnetism); others have a much more complex relationship with an applied magnetic field (spin glass behavior and antiferromagnetism). Substances that are negligibly affected by magnetic fields are known as non-magnetic substances. They include copper, aluminum, gases, and plastic.
The magnetic state (or phase) of a material depends on temperature (and other variables such as pressure and applied magnetic field) so that a material may exhibit more than one form of magnetism depending on its temperature, etc.
- Figure1.Representative figures for ferrimagnetism
1.2. n-Vector Models
There are different types of approaches to model magnetic behaviors of atomic sites for each dimension case. Classical Heisenberg model is the one for three dimensional models we will use the formulations of X_Y model to calculate since our case is two dimensional.
1.2.1. Classical Heisenberg Model
Heisenberg model is one of the n-vector models of statistical mechanics, under which spins are shown as the vertices of x-y dimensions. Classical formulation is given as the following;
![]()
provided that
 .
.
1.3. Monte Carlo Simulation
Monte Carlo method is a probabilistic approach to solve complicated and analytically hard labor problems by generating random inputs over the domain which is interest of calculation. Idea behind the Monte-Carlo simulation was the need of laborious equations to develop atom bomb within the boundaries of Manhattan project, Los Alamos National Lab during 1940’s.
It is basically composed of four simple steps and those are;
- defining a domain of possible inputs,
- generating initial values from randomly distributed inputs,
- perform the equation which will govern the interest of field,
- collecting results.
Calculation that was run is based on the mean field approximation. Mean field approximation is a tool of mean field theory, also called self-consistent field theory, has the main idea that to evaluate one particle in a multi body environment (at which every particle interact with each other), focuses only to one particle and assumes that most important contribution of interaction to that particle through nearest-neighboring particles. These theory used in many field to overcome computational challenges such as Landau theory in physics or molecular dynamics simulations and etc.. In this case, for spin interactions same is considered to be used.
2. COMPUTATIONAL STUDY
2.1. Generic of the Code
To simply sum up the function of code;
1) Define and grid for 2 dimensional case,
2) Assign the initial values for extensive and intensive parameters which belong to entire field.
3) Define randomly distributed input values for (theta),
4) Provide initial conditions to describe theta values over entire field.
5) MT _1 ) defining a domain of possible inputs
6) Providing boundary conditions for the field (to round along the x axis)
7) Provide the equation which will conduct for the domain of possible inputs,
8) Aggregate the results as plots of ‘susceptibility’ and ‘average magnetic moment’ vs. desired temperature values.
2.2. Initial Conditions
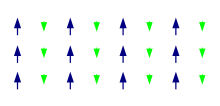
Initial conditions of the field has the following properties. At O K ,all the spins in bravais lattice are orientated towards to applied external magnetic field in ferromagnetic materials which is shown below at Figure2.
When temperature goes higher than O 0K, atoms jiggle and start to deviate from their orientated magnetic field direction through Boltzmann distribution. Figure3 and Figure4 shows this for two different temperatures.
In Figure3 Temperature –magnetic field fight causes domains to be formed. It is an issue of which force will overcome on another. Here, number of iterations is less, so that we have taken Figure 3 and Figure 4 as representative figures.
Boundary conditions are defined on the system in the form of rounding the material along x axis and forming a cylindrical surface. So that, probabilistic calculations over the entire field will be run uninterruptedly and there will be no edge effect based on x axis boundaries.
2.3. Curie Temperature
For any ferromagnetic material, there is a temperature above that material becomes paramagnetic material which has no net dipole moment in total. This is a characteristic temperature for all ferromagnets. The code was run for 10-20 and 30 cells, respectively. Results collected from these runs are shown in Figure 5 and Figure 6. Those graphs are taken from the simulations has the following properties. Number of iteration is 250×60.000 = 15.000.000. H=50,J=1000 and temperature is increased from nearly 0 0K to 2500 0K with 50 degree increments. As it is seen from the graphs, Curie temperature is not clear to be determined since saddle point along exponential is not obvious. Also, at different thicknesses, no significant difference is observed on magnetic field and susceptibility as well.
So, the same simulation for only 10 cell is run for twice iteration number and the results can be shown at Figure7. As it is seen, there is no difference between two iteration number, meaning that associated iteration number is high enough to reach hypothetical equilibrium condition for spin components.
Then, same cod is run for the different set of thicknesses. 5-12-19 are chosen as cell numbers. Figure 8 and Figure 9 show the Magnetization vs. Temperature and Susceptibility vs. Temperature graphs. As seen, even though general behavior of curve is not as we expect, there is decrease at temperature for 5cell, but again almost no difference between 12 and 19 cells.
At the evaluation of these results, determining the Curie temperature is done by linear fit on the temperature range of 900-1400. It is hard to specify exact Curie temperature with such a broad temperature range but linear curve fitting is done to visualize the difference between 5 cell and 12 cell structure. Curve fitting is done around 900 and 1400 K region. Middle point as 1153 K selected to compare average dipole moment of different thicknesses. Figure 10 and Figure 11 show curve fitting for these cells in a row.
3. CONCLUSIONS
All the simulations we run so far are performed by heating the magnetic system from approx. 0K to 2500 K and they should have been completed by giving an exact or near-exact temperature value as Curie Temperature but it is seen that no matter what the input thickness values, decay in the first region (before Tc) is fast such that magnetic field effect is easily deteriorated by increase in temperature. At the thicknesses of 10-20-30 cell, observing the thickness effect was not even close but in the 5-12-19 thicknesses result is promising.
However, all these simulations keep the decay in the first region as an exclamation mark. For further studies, effect of magnetic field with the same parameters can be studied.
References
http://www.vertex42.com/ExcelArticles/mc/MonteCarloSimulation.html
http://en.wikipedia.org/wiki/N-vector_model
M.A. White, “Properties of Materials” (Oxford University Press 1999)
Could you please send the code of Curie temperature calculations by Monte Carlo simulation using Heisenberg model.